课堂上,我们一起探究有一个公用的顶点的多个角的数法。
数的时候为了做到不重复不遗漏,我们先给每条线标上数字,方便按照一定的顺序来数。
一、耐心数角。
(1)从1号线出发,1号和2号组成了一个角,1号还可以和3号线组成角。这样,从1号线出发,能组成2个不同的角。接着,从2号线出发,2号和3号线组成一个角。这样,从2号线出发能组成1个角。
有3条线的时候,一共能组成2+1=3个不同的角。
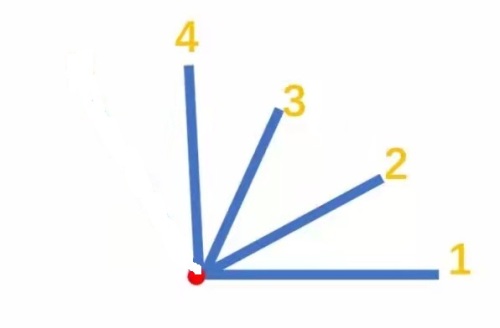
(2)从1号线出发,1号和2号组成了一个角,1号还可以和3号线、4号线组成角。这样,从1号线出发,能组成3个不同的角。接着,从2号线出发,2号和3号线组成一个角,2号还可以和4号线组成角。这样,从2号线出发能组成2个不同的角。从3号线出发,3号和4号线能组成1个角。
有4条线的时候,能组成3+2+1=6个不同的角。
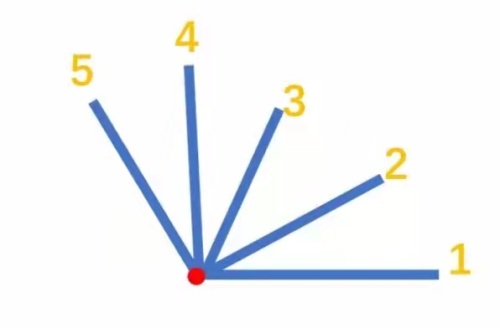
(3)从1号线出发,1号和2号组成了一个角,1号还可以和3号线、4号线、5号线组成角。这样,从1号线出发,能组成4个不同的角。接着,从2号线出发,2号和3号线组成一个角,2号还可以和4号线、5号线组成角。这样,从2号线出发能组成3个不同的角。从3号线出发,3号和4号线能组成一个角,还可以和5号线组成角。这样,从3号线出发能组成2个不同的角。从4号线出发,4号线和5号线组成1个角。
有5条线的时候,一共能组成4+3+2+1=10个不同的角。
二、探究规律。
请你仔细观察计算一共有多少角的加法算式有什么规律呢?
2+1=3
3+2+1=6
4+3+2+1=10
加数都是连续的数,一次比一次少1。
请你仔细观察线的总条数和加法算式中的第一个加数有什么关系呢?总条数和加法算式中加数的个数有什么关系呢?
总条数比总条数和加法算式的第一个加数多1,加法算式的第一个加数比总条数少1。总条数比加法算式中加数的个数多1,加法算式中加数的个数比总条数少1。
三、运用规律。
你能用我们发现的规律数角吗?如果变成6条线,你能直接列算式计算吗?
四、优化思维。
我们可以用八个字来描述数角的过程:数线(数出来一共有几条线),减1(用总条数减1得出得数),倒数(从得数开始倒着数数),相加(把所有倒数的数加起来)。
如果变成7条、8条,你会用我们发现的规律数角吗?







 举报
举报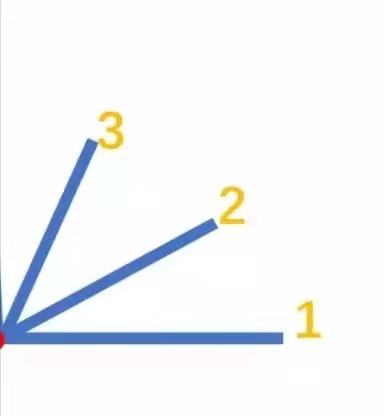

 推荐
推荐 收藏
收藏
